10158. Find the centroid
Find any centroid
in the tree.
Input. The first line
contains one integer n (1 ≤ n ≤ 2 * 105), representing the
number of vertices. Each of the following n – 1 lines
contains two integers vi and ui (1 ≤ vi, ui ≤ n), representing vertices connected by an edge.
It is guaranteed
that the graph is a tree.
Output. Print the number of
a vertex that is a centroid. If there are multiple centroids, print any one of
them.
|
Sample input |
Sample output |
|
12 1 3 2 3 3 4 4 5 4 6 6 7 6 10 10 11 10 12 6 8 8 9 |
6 |
SOLUTION
dfs - centroid
Algorithm analysis
Consider a tree
with n vertices.
A centroid
of a tree is a vertex whose removal results in splitting the tree into
connected components, each containing no more than n / 2 vertices. The
task is to find all centroids of the tree.
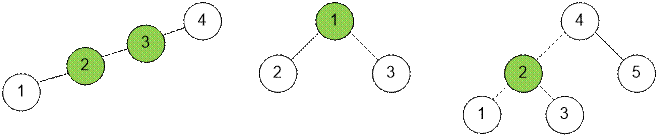
Let’s consider
examples of trees and their centroids (marked in green).
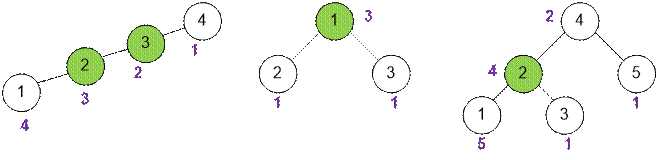
Run a depth-first
search starting from vertex v, which will calculate the number of vertices
in the subtree rooted at vertex v and store this value in sub[v].
For the given examples, we will indicate the corresponding value of sub[v]
next to each vertex v. In all examples, the depth-first search starts
from vertex 1.
If vertex v has children
to1, to2, …, tok , then
sub[v] = 1 + sub[to1] + sub[to2] + … + sub[tok]
Vertex v is a
centroid
of the tree if and only if:
·
for each of its children to, it holds that sub[to]
≤ n / 2;
·
if we remove the
subtree rooted at v
from the tree, the resulting tree contains no more
than n / 2 vertices: n – sub[v]
≤ n / 2;
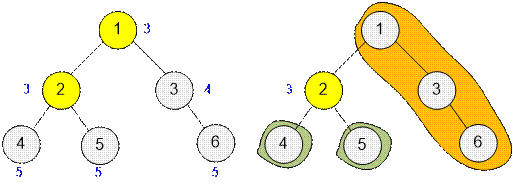
For example, in the tree from the right with n = 5 vertices, vertex 2 is a centroid because:
·
sub[4] = 2 ≤ n / 2;
·
sub[3] = 1 ≤ n / 2;
·
n – sub[2] = 5 – 4
= 1 ≤ n / 2;
Example
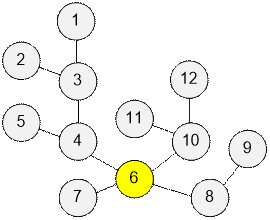
Let’s consider the tree
from the example. Vertex 6 is a centroid.
Algorithm implementation
We’ll store the
graph in the adjacency list g.
vector<vector<int> > g;
The dfs function returns the number
of vertices in the subtree rooted at vertex v and saves this value in
sub[v].
int dfs(int v, int p = -1)
{
sub[v] = 1;
for (int to : g[v])
if (to != p) sub[v] += dfs(to, v);
return sub[v];
}
The centroid function performs
a depth-first search, finds the centroids, and stores them in the centr array.
void centroid(int v, int p = -1)
{
Set flag = 1 if vertex v is a centroid.
int flag = 1;
Iterate through the vertices to, adjacent to v. Consider an
edge v
→ to.
for (int to : g[v])
if (to != p)
{
If for a child to
it holds that sub[to]
> n / 2, then v is not a
centroid.
if (sub[to] > n / 2)
flag = 0;
If for a child to
it holds that sub[to] < n / 2, then the subtree
rooted at to does not contain centroids. It makes sense to continue the
search in the child to only if sub[to]
≥ n / 2.
if (sub[to] >= n / 2)
centroid(to, v);
}
The tree without
the subtree rooted at v contains n –
sub[v] vertices. If it contains more than n / 2 vertices, then v is not a centroid.
if (n - sub[v] > n / 2) flag = 0;
If vertex v
satisfies all the conditions of a centroid, add it to the centr array.
if (flag) centr.push_back(v);
}
The main part of
the program. Read the input data and initialize the arrays.
scanf("%d", &n);
g.resize(n + 1);
sub.resize(n + 1);
Read the input graph.
for (i = 0; i < n - 1;
i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Run a depth-first
search and find the centroids of the tree.
dfs(1);
centroid(1);
Print one of the
centroids.
printf("%d\n", centr[0]);
Algorithm
implementation – second solution
Let’s run a
depth-first search dfs(v), that will compute the following values for
each vertex v:
·
sub[v] contains the number of vertices in the
subtree with vertex v.
·
f[v] contains the maximum size of a subtree
among all subtrees of vertex v, including the subtree containing the
parent vertex of v.
Then, the centroid
will be the vertex v with the smallest value of f[v]. There may
be either one or two such vertices in the tree.
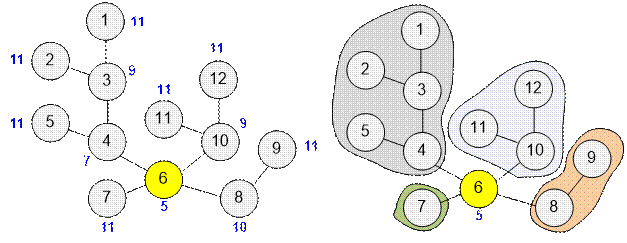
Vertex v = 6 is connected to 4 subtrees, with sizes 1, 2, 3, and 5 respectively.
The value f[6] = 5 contains the maximum size of a subtree.
At the same time,
the smallest value in the array f is f[6] = 5. Therefore, vertex 6 is
the centroid.
Let’s consider the
labeling of a tree with two centroids.
Two vertices have the smallest value in the array f:
f[1] =
3 and f[2] = 3.
void dfs(int v, int p = -1)
{
sub[v] = 1;
f[v] = 0;
for (int to : g[v])
if (to != p)
{
dfs(to, v);
sub[v] += sub[to];
f[v] = max(f[v], sub[to]);
}
f[v] = max(f[v], n - sub[v]);
if ((root == 0) || (f[v] < f[root])) root = v;
}
The main part of
the program. Read the input data and initialize the arrays.
scanf("%d", &n);
g.resize(n + 1);
f.resize(n + 1);
sub.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a,
&b);
g[a].push_back(b);
g[b].push_back(a);
}
Run a depth-first
search and print one of the centroids root
of the tree.
root = 0;
dfs(1);
printf("%d\n", root);
Python implementation
Increase
the size of the stack.
import sys
sys.setrecursionlimit(300000)
The dfs function returns the number
of vertices in the subtree rooted at vertex v and saves this value in
sub[v].
def dfs(v, p = -1):
sub[v] = 1
for to in g[v]:
if to != p:
sub[v] += dfs(to, v)
return sub[v]
The centroid function performs
a depth-first search, finds the centroids, and stores them in the centr array.
def find_centroid(v, p = -1):
Set flag = True if vertex v is a centroid.
flag = True
Iterate through the vertices to, adjacent to v. Consider an
edge v
→ to.
for to in
g[v]:
if to == p: continue
If for a child to
it holds that sub[to]
> n / 2, then v is not a
centroid.
if sub[to] > n // 2:
flag = False
If for a child to
it holds that sub[to] < n / 2, then the subtree
rooted at to does not contain centroids. It makes sense to continue the
search in the child to only if sub[to]
≥ n / 2.
if sub[to] >= n // 2:
find_centroid(to, v)
The tree without
the subtree rooted at v contains n –
sub[v] vertices. If it contains more than n / 2 vertices, then v is not a centroid.
if n - sub[v] > n // 2:
flag = False
If vertex v
satisfies all the conditions of a centroid, add it to the centr array.
if flag: centr.append(v)
The main part of
the program. Read the input data and initialize the arrays.
n = int(input())
g = [[] for _ in
range(n + 1)]
sub = [0] * (n + 1)
centr = []
Read the input graph.
for i in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Run a depth-first
search and find the centroids of the tree.
dfs(1)
find_centroid(1)
Print one of the
centroids.
print(centr[0])
Python implementation – second
solution
Increase
the size of the stack.
import sys
sys.setrecursionlimit(200000)
Let’s run a
depth-first search dfs(v), that will compute the following values for
each vertex v:
·
sub[v] contains the number of vertices in the
subtree with vertex v.
·
f[v] contains the maximum size of a subtree
among all subtrees of vertex v, including the subtree containing the
parent vertex of v.
Then, the centroid
will be the vertex v with the smallest value of f[v]. There may
be either one or two such vertices in the tree.
def dfs(v, p=-1):
global root
sub[v] = 1
f[v] = 0
for to in g[v]:
if to != p:
dfs(to, v)
sub[v] += sub[to]
f[v] = max(f[v], sub[to])
f[v] = max(f[v], n -
sub[v])
if root == 0 or f[v] <
f[root]:
root = v
The main part of
the program. Read the input data and initialize the arrays.
n = int(input())
g = [[] for _ in range(n + 1)]
f = [0] * (n + 1)
sub = [0] * (n + 1)
for _ in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Run a depth-first
search and print one of the centroids root
of the tree.
root = 0
dfs(1)
print(root)